
大学入試の数学で、たまにザワつく問題というのがあります。
先日行われた2021年一橋数学 大問[1]がまさにザワつく問題でした。中学受験生の小学生にも無理なく解ける問題なので、ご紹介します。
ざわつく2021年一橋数学 大問[1] 素数問題
ざわつく問題とは?
簡単に言ってしまうと見た瞬間「は?」「ん、んん!」となる問題です。
・問題文がやたら短い。
・問われている内容が簡単だったり小学生でも解けるが、入口を間違うとハマったり、とんでもない別解がある。
有名なのは、「円周率が3.05より大きいことを証明せよ」(東大)とか、「tan1°は有理数か?」(京大)とかです。問題文が1行だけなので受験生は「は?これだけ?」となります。
2021年一橋大学数学【1000以下の素数は250個以下であることを示せ】
1行これだけです。インパクトがある問題でざわついています。算数、数学が苦手な人でも、小学生でも解けそうだというのは感覚的に理解できるのではないでしょうか?
またパッと見、全部数え上げる方法でもイケるのでは?と思う人もいるかもしれません。
小学生でもわかる解答
問「1000以下の素数は250個以下であることを示せ。」
→1000以下の自然数(1以上の整数)で素数以外のものを750個示せばよい。(これがゴール)
①2の倍数:1000以下の2の倍数は500個。2は素数なので、500-1=499個は素数ではないことが確定。
②3の倍数であり2の倍数でない:1000以下の3の倍数かつ2の倍数でないもの
333(3の倍数)-166(3の倍数だが2の倍数でもある→6の倍数)=167個。3は素数なので、167-1=166個は素数はないことが確定。
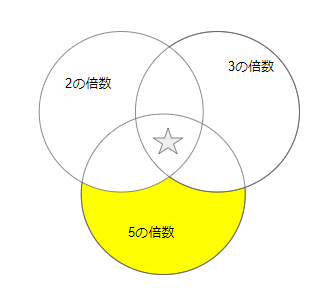
③5の倍数であり①または②に含まれないもの(下図の黄色)を数える。ベン図を使うのが良いです。
→5の倍数の個数-(5の倍数かつ3の倍数の個数)-(5の倍数かつ2の倍数の個数)+(5の倍数かつ2の倍数かつ3の倍数→図の☆の部分)
=200-66-100+33=67個、5は素数なので67-1=66個は素数ではないことが確定。
④ ①~③より499+166+66=731個は1000以下で素数ではない数。
⑤ゴールは「1000以下で自然数で素数以外のものを750個示す」なので、後19個、素数でないものを見つけられれば良い。
⑥①~④で2,3,5の倍数に注目したので、それより大きい素数7,11,13,17,19,23,29,31…の倍数について考えます。これらを2つ掛け合わせた数は(当然)素数ではありません。
たとえば7x11や7x13, 11x13…また同じ数を掛け合わせた7x7も素数ではありません。
(故に8x8=64個は素数以外の数があるのがわかります…が一応列挙します)
31x31は961と1000近くになるので注意です、31以下の素数を掛け合わせた数をカウントするために、列挙します。
・7x7,7x11,7x13,7x17,7x19,7x23,7x29,7x31(8個)
・11x11,11x13,11x17,11x19,11x23,11x29,11x31(7個)
・13x13,13x17,13x19,13x23,13x29,13x31(6個)…
ここまでで21個、また1も素数でないため少なくとも22個は1000以下でかつ、①~③で数えたものとは別の「素数でない数」が存在する。
①②③⑥、つまり731+22=753個、1000以下の自然数で素数でない数が少なくとも753個存在する→1000以下の素数は250個以下である。(おわり)
ちなみに1000以下の素数は168個です。
序盤で基本に沿って2,3,5…と進めていき最後は数え上げと中学受験を彷彿とさせる問題です。中学受験の数え上げはもっとキツイものもありますね。
この問題、河野玄斗さんも取り上げていて「伝説も問題になりそう」とコメントしています。https://www.youtube.com/watch?v=MQrHL1T1Ihw
意外な解き方
中学受験範囲ではないのでマニア向けですが、この問題についてオイラー関数を使って、1行ほどで証明できる方法が見つかっています。大学入試数学解説:一橋2021年第1問【整数問題】 https://www.youtube.com/watch?v=wi3PTAdFTSQ この動画の後半で解説しています。
参考になりましたら、応援クリックしていただけると嬉しいです。
↓ ↓ ↓ ↓