
タイトルの通り、ある私立中学の算数の入試問題で「気になることを書け!」という、深いというか、なかなか面白い問題がありましたのでご紹介します。この学校は毎年最後に面白い問題を出題しています。
算数の入試問題で「気になることを書け!!」
麗澤中学の2021年入試問題大問[4]の(3)の設問が「気になることを書きなさい」という面白い設問になっています。

どういうことでしょうか?
この問題は
2021年07月 麗澤中学校【算数】 | 日能研 シカクいアタマをマルくする。
にも取り上げられています。
解答編
(1)から解いていきましょう。
設問(1) 1÷3を分数と少数で表しなさい。ただし、小数は小数第3位まで答え、それ以降も続く場合は「…」をつけて答えなさい。
解答→(1) 分数:1÷3=1/3 小数:1÷3=0.333…
設問(2) 2つの数AとBが等しいとき、その2つの数にある数Cをかけた2つの数AxCとBxCは等しいか等しくないか答えなさい。
解答→等しい数に同じ数をかけると、結果は等しくなる。なので、AとBが等しければ、A×CとB×Cも等しくなる。
設問(3) (1)で求めた分数と小数のそれぞれに3を書けた数を比べて気になることを(2)をふまえて書きなさい
解答→1/3と0.333…は、どちらも1÷3の計算結果ですが、それぞれに3をかけた場合、
(1/3) x 3 =1
0.333…×3=0.999…
となり、同じになっていない。
日能研はこの問題を取り上げた理由を
この問題は、「不思議だな」「変だな」「気になる」と子どもの中からわき上がる気持ちを受け止める問題です。算数の問題を解く力だけでなく、探求の第一歩となる「?」を大切にしたいという意図が伝わってきます。
普通算数の問題は、答えを一つ出せという問題ですが、この問題は「気になることを書け」という「?」(疑問)を持つことが大事でそれを書かせるという珍しい設問になっています。
実はこれ2020年の問題のほうがさらに面白いのです
これも「気になることを書け」という問題です。
2020年麗澤中の算数も「気になることを書け」

この問題、ワンダーラボというサイトの2020年良問大賞の一つとして挙げられています。→ ワンダーラボ 中学入試算数 良問大賞2020 | WeThink
「あまりのある割り算」の答え方について、等号本来の意味からすると正確でない、ということを風刺している問題です。現状の算数教育について、問題提起を行っているようにも思えます。
ワタシの感想としては、これはかなり面白い問題だなと思いました、2021年の問題より面白い。答え自体はそんなに難しくはないと思うのですが、先ほどと同じで、「気になることを答えなさい」という設問が個性的です。矛盾を指摘することが作問者の意図ですが、「気になること」という「違和感」を問いにしているのがとてもおもしろい。
解答ですが、これ四谷大塚にも解答はないんですよね。
というわけでワタシの解答をのせておきます。間違いではないと思います、満点でなかったらすみません。
解答編
(1)「=」の意味→「=」の左側と右側が同じになるという意味。
[解説]小学生の中には「=」の意味を「答えは」ということと考える人もいますが、よろしくはないです。「=」は等しいものを結ぶための記号で、=の左側と右側、つまり左辺と右辺が等しくなるというのが本質です。
たとえば、半径12の円の面積を出す場合に
12x12=144 x3.14 = 452.16 みたいな計算式を書く子がいます。これは左辺=右辺となっていないので間違いです。
「=」を「等しい」ではなく、「答えは」と解釈しているからです。12x12(答えは)144、144x3.14(答えは)452.16 子供がやらかしがちなので注意が必要で、この手の計算プロセスをやる子は計算間違いが多いという特徴もあります。
(2) 「29÷7」の計算結果と、「37÷9」の計算結果が同じ「4あまり1」となっている。
つまり(1)にあてはめると、「29÷7」と「37÷9」が同じという意味になる。
しかし実際は「29÷7」と「37÷9」の計算結果は同じにはならない。
算数の問題で気になること、つまり違和感を答えさせる問題。今まで強く意識していなかったことでも、もう一度意味を考え直してみよう、というメッセージにも読めます。またワンダーラボのコメントにありますが、算数教育に対して風刺というか問題を投げかけているようにも見えてきます。
補足。この問題解答用紙を見ると解答欄がとても大きいんですよね、この問題に対しての気づきをたくさんかいて欲しいという学校の思いがあらわれているかもしれません。

2019年最終問題と解答も面白い!!
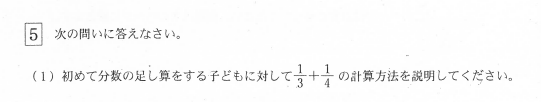
初めて分数の足し算をする子どもに対して、1/3 + 1/ 4の計算方法を説明してくださいという問題で、これは通分の考え方をどう説明するかがポイントです。
[解答]後で紹介する日能研も同じ方法ですが、ピザを使うやり方がいいです。
・3分の1→丸いピザを3等分したうちの1つ
・4分の1→丸いピザを4等分したうちの1つ
大きさが違うので、12等分することで同じ形のピースに揃えて数えることができる
3分の1→丸いピザを3等分したうちの1つ→丸いピザを12等分したうちの4つ分
4分の1→丸いピザを4等分したうちの1つ→丸いピザを12等分したうちの3つ分
3分の1と4分の1を足すということは、12等分にしたピザだと4+3で7個分
という考え方です。
日能研のシカクいあたまをマルくするにも取り上げられています。図があるので解答はこちらのほうがわかりやすいと思います。
2019年05月 麗澤中学校【算数】 | 日能研 シカクいアタマをマルくする。
今日取り扱った2題を出題した麗澤中学は千葉にある私立中学で四谷大塚の偏差値ではアドバンスドのクラスが54程度、通常クラスが48程度と極端に難易度が高い中学というわけではありません。そしてこの2題の問題は難関中学で出るような難問ではありませんが、問題集を解くだけでは答えるのが難しい問題です。難問を解ける必要はないけど、ちょっとした算数のことに興味を持てる子、面白いなと思ってもらえる子に入学して欲しいというのが学校の主張だと考えます。
今回はここまでっす。